

The atoms have been given different labels to allow us to follow their transformations. Property of a shape with one or more lines of symmetry. We can define the x-axis to run through the carbon-carbon double bond while the y-axis bisects this bond at right angles. The planar molecule ethene provides a simple example to demonstrate the effects of the symmetry elements described above. Molecular symmetryĭetermining the symmetry elements present in a molecule involves considering which rotations, reflections and inversions will leave the shape of the molecule unchanged even though individual atoms will have moved, the final result must be indistinguishable from the starting structure. The inversion symmetry element is denoted by the symbol i. In this case this is the same as a 180° rotation, but generally these two operations may give different results. This means that our original point moves from (1,2) to (–1,–2). The inversion operation simply reverses the sign on all the coordinates. We could clearly rotate a point through any angle, but the transformation of the coordinates will be harder to describe. Thus, the absolute value of both 2 and –2 is 2. Note that where the absolute value of a number is referred to, this is simply its magnitude without taking account of whether it is positive or negative. If we can understand the behaviour of individual points when symmetry operations are applied, and identify appropriate symmetry elements (mirror planes, rotational axes and inversion centres), then we will be able to combine several points and study molecules. We saw in a previous article 6 that the position of any point (and consequently any atom) can be defined in terms of its x and y coordinates, denoted as ( x, y). 4 Ji-Won Son from the State University of New York in Buffalo, US, has also suggested that there is confusion between reflection and rotation among both students and pre-service teachers. Xenia Xistouri and Demetra Pitta-Pantazi from the University of Cyprus have suggested students’ mathematical performance in reflective symmetry tasks can be predicted by their general mathematical achievement, perspective taking abilities and spatial rotation abilities, in descending order of importance. However, more homemade teaching aids can be just as effective, for example: a collection of objects showing different symmetry a magnet-backed mirror and a set of modified molecular models and a frame to demonstrate different symmetry axes.
1 Recent advances in 3D printing provide interesting opportunities in this area. Teaching aidsĮxtending these principles to three dimensions is much easier using molecular models, and hand-held models probably have an advantage over computer generated ones. The way that simple symmetry elements apply to molecular structures can be introduced by working in two dimensions and considering planar molecules.
Order 2 implies a duplicate image at a rotation of 180º (splitting 360º into 2 equal parts).
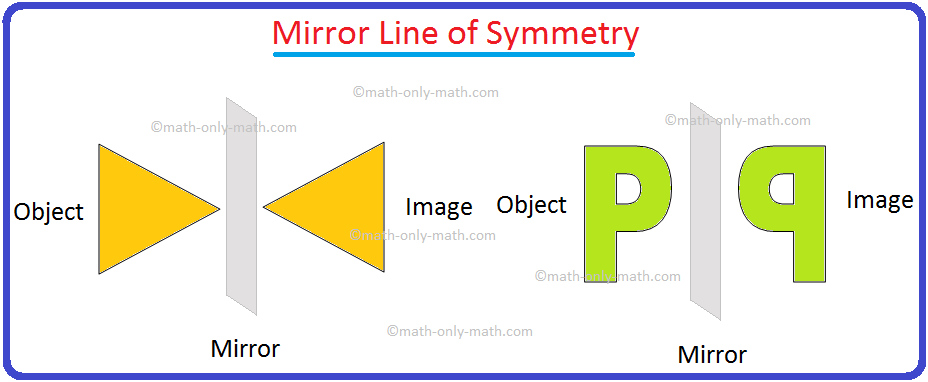
LETTERS WITH REFLECTION SYMMETRY FULL
Order 1 implies no true rotational symmetry exists, since a full 360 degree rotation is needed to again display the object with its original appearance. The angles of 0º and 360º are not listed as they are the starting locations.When determining order, the last rotation returns the object to its original position (360º). The number of positions in which the object looks exactly the same is called the order of the symmetry. The angles of rotational symmetry will be factors of 360. The angles of 0º and 360º are excluded since they represent the original position (nothing new happens). A geometric figure has rotational symmetry if the figure is the image of itself under a rotation about a point through an angle whose measure is strictly between 0º and 360º.


 0 kommentar(er)
0 kommentar(er)
